一、引入问题
DR_CAN:现实生活中,由于因果定律的存在,所有的传递函数都是真分数(式)。
一个更常见的陈述是:“现实生活中传递函数的分母阶数 必不小于分子阶数 ”。
本文尝试说明其原因。
二、展开说明
(一)一阶微分环节
我们讨论一个最简单的假分式传递函数:
这是一个一阶微分环节,我们对它进行 逆变换。
我们(自动控制中)好像从来没有对
进行过反变换,即使它看起来很简单。实际上
并不容易求得,但我们可以换个思路:
| 函数 |
时域 |
拉普拉斯 域 |
| 单位冲激函数 |
|
|
| 单位阶跃函数 |
|
|
| 斜坡函数 |
|
|
这是一个拉普拉斯变换表,容易发现:“向上是求导,向下是积分”。
按照这种规律来看 应该在
的头顶,那么在时域中就需要对单位冲激函数 求导:
被称为冲激偶。
我们先把拉普拉斯变换表补全:
| 函数 |
时域 |
拉普拉斯 域 |
| 单位冲激偶 |
|
|
| 单位冲激函数 |
|
|
| 单位阶跃函数 |
|
|
| 斜坡函数 |
|
|
由 求导得来:
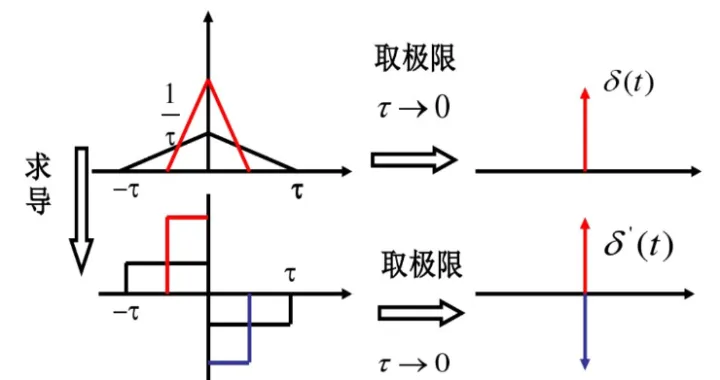
它的取值情况:
(二)响应
对于 :
- 单位冲激响应
当输入为
时,我们心里默念:系统的单位冲激响应是它的传递函数的拉普拉斯逆变换,所以此时输出就是冲激偶。
上文中讲到冲激偶
的取值是和
之后有关的,或者说:
时的输入会影响到
时的输出。
这是违背因果律的。
- 单位阶跃响应
我们考虑当输入
也就是 时: 此时输出为单位冲激响应,单位冲激响应也是与 之后有关的,同样违背因果律。
三、数学中
观察拉普拉斯变换表,
相当于微分算子,考虑一个求导过程: 时刻的导数和
有关,从这里也可以看出不符合因果定律。
四、电路中
考虑一个电感器件: 在电路的 域模型中:
在形式上它确实是一个微分环节,但现实中由于电感绕线电阻的存在使得它实际上是个惯性环节。
换个方向,我们可以如此定义电感:
以电压差输入,以电流为输出,这样传递函数就是一个积分环节。
同样的,考虑一个电容器:
域中:
我们可以这么写: 时域中: 这是容易理解的,电流 的流动使得电荷
在电容器以某种状态分布,从而产生了电势差。
