使用control库绘制控制系统相关图象

一、前言

我经常需要绘制根轨迹、Nyquist 图之类的图象，MATLAB 启动确实是有点慢，可以使用 Python 的 control 库来迅速的画出所需的图象。

下面是简单的例子。

二、画图

（一）准备工作

  1. 安装 control 库： 
    1
    pip install control
  2. 导入所需要的库

下面的库都是后续操作所要使用的： 

1
2
3
4
5
import control as ctrl
import numpy as np
import matplotlib.pyplot as plt
import sympy as sp
from functools import reduce
3. 定义 tf2latex 函数

tf2latex 用于将传递函数转换成 LaTeX 字符串，方便后续使用。 

1
2
3
4
5
6
7
8
9
10
# Transfer Function 2 LaTex
def tf2latex(sys):
    # Transfer Function to sympy expression
    s = sp.symbols('s')
    num = sp.Poly(sys.num[0][0], s).as_expr()
    den = sp.Poly(sys.den[0][0], s).as_expr()
    sys_expr = num / den
    # sympy expression to LaTex
    sys_latex = sp.latex(sys_expr)
    return sys_latex

（二）系统响应

对于闭环传递函数为 的系统，绘制其单位冲激响应 和 单位阶跃响应 ：

  1. 定义绘图函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Draw Impulse Response
def impulse_response(sys, T):
    title = f'Impulse Response of $' + tf2latex(sys) + '$'
    t, y = ctrl.impulse_response(sys, T)
    plt.plot(t, y)
    plt.title(title, y=1.05)
    plt.xlabel('Time (s)')
    plt.ylabel('Impulse Response')
    plt.grid()
    plt.show()

# Draw Step Response
def step_response(sys, T):
    title = f'Step Response of $' + tf2latex(sys) + '$'
    t, y = ctrl.step_response(sys, T)
    plt.plot(t, y)
    plt.title(title, y=1.05)
    plt.xlabel('Time (s)')
    plt.ylabel('Step Response')
    plt.grid()
    plt.show()
  1. 定义传递函数并绘图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Define Transfer Function
# K, Numerator and Denominator
K = 1

num = [
    [16]
]

den = [
    [1, 10, 16]
]

num[0] = [K * i for i in num[0]]

# Use functools.reduce to automatically calculate the convolution of multiple polynomials
num_conv = reduce(np.convolve, num)
den_conv = reduce(np.convolve, den)
sys = ctrl.TransferFunction(num_conv, den_conv)

# Draw
step_response(sys, np.linspace(0, 5, 1000))
impulse_response(sys, np.linspace(0, 5, 1000))
  1. 图象

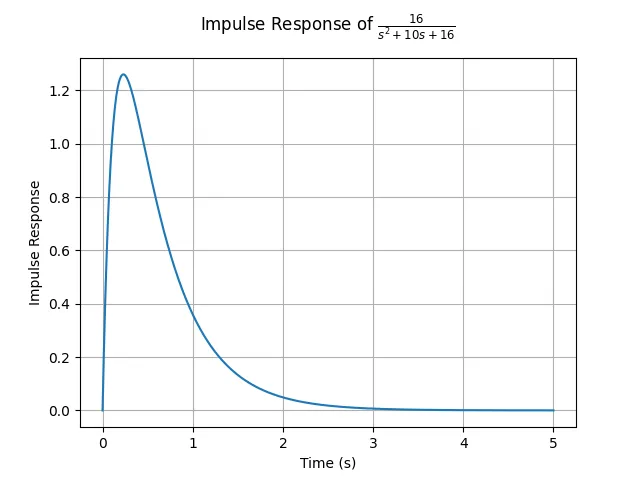
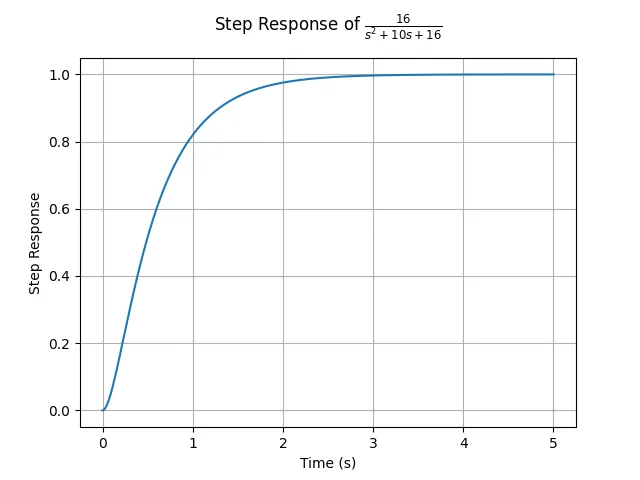
（三）根轨迹

对于开环传递函数为 的系统，绘制其根轨迹：

  1. 定义函数 

    1
    2
    3
    4
    5
    6
    # Draw Root Locus
    def root_locus(sys):
        title = f'Root Locus of $' + tf2latex(sys) + '$'
        ctrl.root_locus(sys, title='')
        plt.title(title, y=1.05)
        plt.show()

  2. 定义传递函数并绘图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Define Transfer Function
# K, Numerator and Denominator
K = 1

num = [
    [1]
]

den = [
    [1, 0],
    [1, 8, 20]
]

num[0] = [K * i for i in num[0]]

# Use functools.reduce to automatically calculate the convolution of multiple polynomials
num_conv = reduce(np.convolve, num)
den_conv = reduce(np.convolve, den)
sys = ctrl.TransferFunction(num_conv, den_conv)

# Draw
root_locus(sys)
  1. 图象

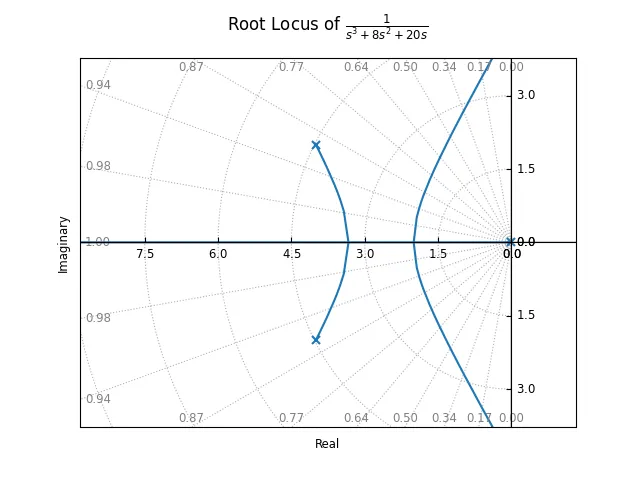
（四）Bode 图

对于开环传递函数为 的系统，绘制其 Bode 图：

  1. 定义函数
1
2
3
4
5
6
# Draw Bode Plot
def bode_plot(sys):
    title = f'Bode Plot of $' + tf2latex(sys) + '$'
    ctrl.bode_plot(sys, title='')
    plt.title(title, y=1.05)
    plt.show()
  1. 定义传递函数并绘图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Define Transfer Function
# K, Numerator and Denominator
K = 1

num = [
    [1]
]

den = [
    [1, 0],
    [1, 8, 20]
]

num[0] = [K * i for i in num[0]]

# Use functools.reduce to automatically calculate the convolution of multiple polynomials
num_conv = reduce(np.convolve, num)
den_conv = reduce(np.convolve, den)
sys = ctrl.TransferFunction(num_conv, den_conv)

# Draw
bode_plot(sys)
  1. 图象

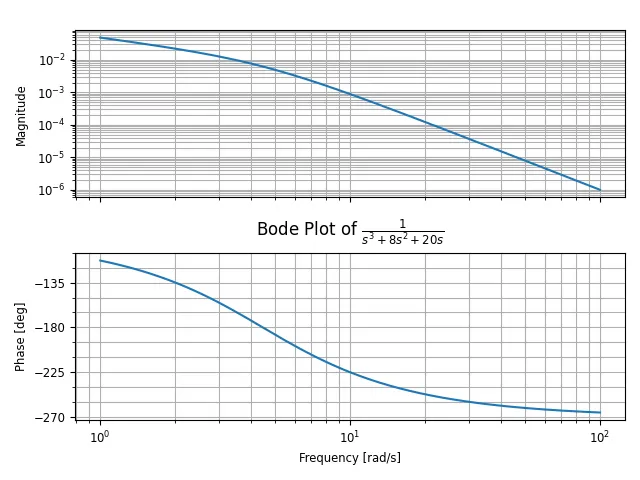
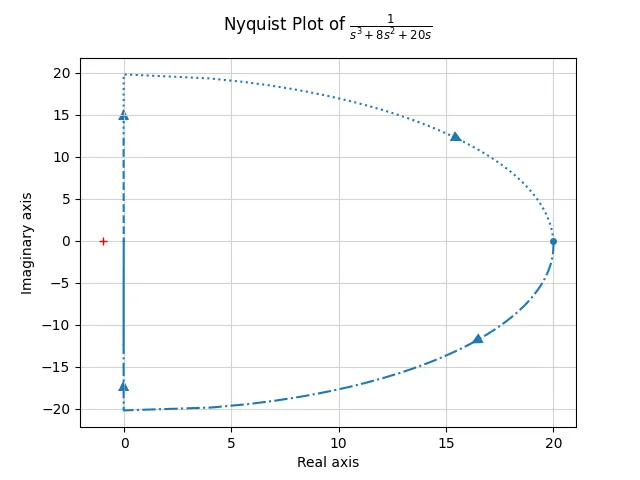
（五）Nyquist 图

对于开环传递函数为 的系统，绘制其 Nyquist 图：

  1. 定义函数
1
2
3
4
5
6
# Draw Nyquist Plot
def nyquist_plot(sys):
    title = f'Nyquist Plot of $' + tf2latex(sys) + '$'
    ctrl.nyquist_plot(sys, title='')
    plt.title(title, y=1.05)
    plt.show()
  1. 定义传递函数并绘图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Define Transfer Function
# K, Numerator and Denominator
K = 1

num = [
    [1]
]

den = [
    [1, 0],
    [1, 8, 20]
]

num[0] = [K * i for i in num[0]]

# Use functools.reduce to automatically calculate the convolution of multiple polynomials
num_conv = reduce(np.convolve, num)
den_conv = reduce(np.convolve, den)
sys = ctrl.TransferFunction(num_conv, den_conv)

# Draw
nyquist_plot(sys)
  1. 图象

三、说明

完整代码见 barkure/py-control。

dark
sans